Fourth Dimension
While giving someone a definition of the fourth dimension is relatively easy, giving someone an intuitive understanding of the fourth dimension can be quite difficult. A definition of the fourth dimension could go like this: The fourth dimension is all space that one can get to by travelling in a direction perpendicular to three-dimensional space. Whenever an uninitiated person hears this, they start pointing their finger around in the air, trying to figure out how it's possible for such a direction to exist. Such a short explanation gives them no intuitive feeling of the fourth dimension.
In order to give you a better understanding the fourth dimension, I will begin with a method that follows a sequence of n-hypercubes that starts with the zeroth dimension and progresses up to the fourth dimension. An n-hypercube is the generalization of the cube within n dimensions, with a 3-hypercube just being the traditional cube. By seeing each n-hypercube build up from the previous one, you should have a better understanding of the final step, from the third dimension to the fourth dimension.
Step 1 - Zeroth Dimension. Imagine a point in space. It is a 0-hypercube. A point is zero dimensional because it has no width, length, or height, and is infinitely small. Every point is exactly the same and has the same measurements, because it has no dimension. Below is a picture of a point, representing the zeroth dimension.

Step 2 - First Dimension. Take the zero-dimensional point and extrude it in any direction, creating a line segment, which is a 1-hypercube. All line segments are one-dimensional because they differ in size by only one measurement, length. They all have the same width and height, which is infinitely small. If you expanded the line infinitely, it would cover one-dimensional space.

Step 3 - Second Dimension. Now take the line segment and extrude it in any direction that is perpendicular to the first direction, creating a square, which is a 2-hypercube. All squares are two dimensional because they differ with each other in size by two measurements, width and length. They all have the same height, which is infinitely small. All of the edges are the same length, and all of the angles are right angles. If you expanded the square infinitely, it would cover two-dimensional space.
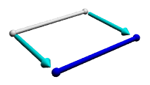
Step 4 - Third Dimension. Take the non-infinite square and extrude it in a third direction, perpendicular to both of the first two directions, creating a cube, which is a 3-hypercube. All cubes are three dimensional because they differ with each other in size by all of the three measurements that we know of - width, length, and height. Just like the square, all of the edges within a single cube are the same length, and all of the angles are right angles. If you expanded the cube infinitely in all directions, it would cover three-dimensional space.
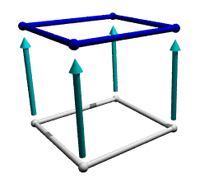
Step 5 - Fourth Dimension. Now, the final step. Take the non-infinite cube and extrude it in yet another direction perpendicular to the first three. But how can we do this? It is impossible to do within the restrictions of the third dimension (which will I refer to as realmspace in this webpage). However, within the fourth dimension , it is possible. The shape that results from this extrusion of a cube into tetraspace is called a tesseract, which is a 4-hypercube. All tesseracts differ from other tesseracts in size by four measurements - width, length, height, and a fourth measurement, which I call trength. Looking back to the previous n-dimensional cubes, they all have the same trength, which is infinitely small. Just like the cube and square, all of the edges within a single tesseract are the same length, and all of the angles are right angles. If you expanded the tesseract infinitely, it would cover four-dimensional space.
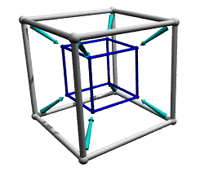
There are several ways to view the tesseract, and I will show three of them here. The first one is called an inner projection, and it is formed from a projecting the tesseract into realmspace with a perspective projection. The parts of the original tesseract that are farther away appear smaller in the inner projection. The original cube cell that existed before the extrusion into a tesseract is in gray, the paths of the vertices are in teal, and the stopping point of the extruded cube cell is in blue. The real tesseract isn't shaped like the inner projection shown below - the inner projection is a very distorted "image" of the original tesseract. All of the edges you see in the image are actually the same length as each other, and all angles between edges are right angles.
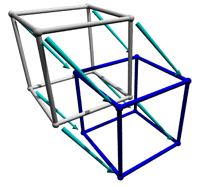
The second way to view a tesseract isn't actually a normal tesseract, but a parallel projection of a skewed tesseract. To make this shape, first you make a tesseract, then shift the top cube cell a short distance in a diagonal direction, parallel to realmspace. Since this shift is parallel to realmspace, it can actually be in any direction that you can point to. After the shift, you trace the shadow of the skewed tesseract's edges. The result is a shape that has two cubes with their vertices connected together. In the orignal shape, all of the edges within the cube cells are the same length and have right angles with each other. However, they don't have right angles with the teal connection edges, and the teal connection edges are slightly longer than the cube cells' edges.
The third way to view a tesseract is a parallel projection into realmspace. It is the same as a skewed tesseract, but without the top cube cell shifted. Since the edges of the tesseract were extruded in a direction perpendicular to realmspace, when the shape is projected back into realmspace, the edges of the blue cube cell are projected straight back onto the gray cube cell's edges. The resulting projection is a simple cube. This didn't happen with the inner projection, because that projection was a perspective projection.

This last step of trying to view a tesseract shows the difficulties in portraying objects from tetraspace within the limitations of realmspace - there is an extra perpendicular direction that we can't depict within our own space without distorting the original object. Because of these problems, it takes many examples in order to begin understanding the nature of the fourth dimension.
four dimensional space) is a fascinating place. Events that would be bizarre and mind-bending to us puny little realmic beings would be common-place and taken for granted in tetraspace. Jumping straight into thinking about tetraspace is enough to boggle any human mind. An indirect route must be taken if there is any hope of understanding the possibilities of tetraspace. The method I use here is the one pioneered by the books Flatland and Sphereland, and is the one used in just about every other text about the fourth dimension. First, the I tell of the adventures of a planar being (a two-dimensional being) attempting to understand realmspace. Going from planespace (two-dimensional space) to realmspace will shed light on how to conceptualize going from realmspace to tetraspace. While going from planespace to realmspace may seem overly simple, it is necessary to understand exactly what is happening so that you can understand the process of going from realmspace to tetraspace.
Just as tetraspace is mind-boggling to us realmic beings, realmspace is mind-boggling to planar beings. Things we take for granted are extremely difficult for planar beings to conceptualize. The only thing a planar being can see of our realmic objects is their planar cross sections in his planespace, and the effects of them rotating. At first, he will only be able to conceptualize the effects in planespace of realmic objects. He will only see planar objects in his mind. Eventually, with much deep thought and introspection, he may be able to conceptualize the realmic object itself. Similarly, when starting to think about tetraspace, we will only be able to conceptualize the effects of tetral (four-dimensional) objects in realmspace. We will only be able to see realmic objects in our mind at first. But, by the effects we see, we can carve a sculpture in our minds of how the full object really looks like, and conceptualize the whole of the tetral object.
The name of our planar subject is "Fred". He lives in a plane called Flatland. The only directions that Fred knows of are forward, backward, up, and down. Fred has no concept of right or left. His viewing area is merely a vertical line. Here is a picture of Fred in his native habitat:
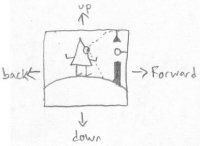
Since Fred's viewing area is only a line, he can't see as much at once as we can. Here is the view that Fred would see if he was in the picture above:
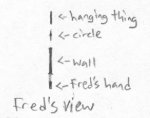
Unfortunately for Fred, he can't see backwards - he can only see forwards. It is impossible for him to simply spin around and face the opposite direction. It is easy for beings in realmspace to face a different direction because they can just spin around, left or right. The only way for beings in planespace to face a different direction though is to turn their head down and heels up. Fred either has to stand upside down to be able to see what is behind him, or he has to walk backwards blind because he only has an eye on his front side.

Fred's writing system is very rudimentary, since a linear surface doesn't allow much detail. His writing system looks somewhat like Morse code. Here is what a page from one of his books looks like, in his view:


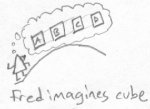
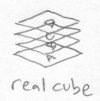
Fred understands the concept of a square. It can be imagined as a series of lines stacked side by side, so that the resulting shape has four sides. He has no concept of what a cube would look like, though. The best he could do is imagine a succession of squares next to each other. As you can see, this is far from the actual representation of a cube. A cube is a series of squares stacked on on top of the other:
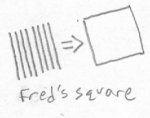
Fred also understands what a circle looks like. It can be imagined as a series of lines stacked side by side in the way that a square is formed, but the lines start small and expand to a certain size, then shrink down again at other side.
Fred can't understand what a sphere really looks like, though. He can imagine it as a series of circles, starting small and expanding, then shrinking down again. Here is how he might picture it:

Or, he might decide to picture it as a group of concentric circles (circles with the same center):


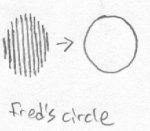
But, as you can see, that's not really what a sphere looks like. Now imagine Fred one day is sitting in his living room, and a sphere from realmspace passes through the air right before his eyes. To him, it will appear as if a circle appeared out of nowhere in front of him. It expands rapidly, and Fred fears that it is going to devour him and his house with him. But to his relief, its growth slows down and stops. Then, the circle starts shrinking again, but slowly. Then it starts to shrink faster and faster until it quickly disappears. Here is what the event looks like:

In realmspace, there is a character named Bob. He is basically your average guy - two legs, two eyes, a brain, all the usual body parts. His view of his world is a 2 dimensional plane, one dimension more than Fred has. Here is Bob in his native habitat, and his view of that habitat:


Since Bob has one dimension more than Fred has, his writing system can be more elaborate. He can write on a 2 dimensional surface. Instead of only one line of text on a page, there can be multiple lines. This allows a lot more text to me stored in a realmic book. Here is what a page from one of his books looks like:

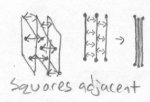
Bob fully understands the concept of a cube. A cube is a sequence of squares laying top to bottom flat on top of each other. For any one square in this cube, every point on one surface of the square touches every other point on the surface of the square above it, and on the other side, touches every point on surface of the square below it. Here is an illustration:
Bob also understands the concept of a sphere. A sphere is a sequence of concentric circles laying top to bottom on each other, as with a square. Like a square, adjacent slices of the circle touch each other at every point. Here is an illustration:

Bob has troubles imagining a tetracube, however. Here is the best he can do to imagine a tetracube:

A tetracube is actually a sequence of cubes, where every part of a cube in this tetracube (all the insides of it) touch all the insides of the cube to its right and to its left (or its up and down, or its front and back). In actuality, the direction of the adjacent cubes are not imaginable in terms of 3d directions. I will call one of the directions into tetraspace Upsilon (for up) and the other Delta (for down).
If Bob was viewing Fred's planar world, he would see that there are two sides to it. Bob could either be on top of Flatland or below it, but in order to get to the other side, Bob must go through Flatland. There is no other way to get to the other side. Planespace separates realmspace into two separate parts. In the same way, a tetral character (Let's call her Emily) would see that she is on one side of realmspace, and she'd have to pass through Bob's world to get to the other side of it. Realmspace separates tetraspace into two separate parts.
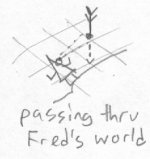
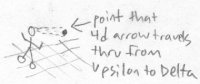
In the first illustration below, an arrow shows the path from one side of Flatland to the other. If the arrow was an object, Fred would only see a small point. In the second illustration, a tetral arrow that passes from one side of realmspace to the other would intersect realmspace with a small point. Bob doesn't see any other part of the arrow but this:
One day, Bob is innocently sitting in his living room (as Fred was that one day), and all of a sudden, in the middle of the air, a sphere appears and grows rather rapidly. Its size levels off at a point, then starts shrinking slowly. Its shrinking quickens until it completely disappears. Bob just experienced the passage of a tetrasphere (four dimensional sphere) through realmspace.
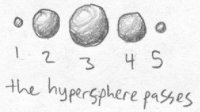
I'm now going to describe in more detail the worlds of Fred, Bob, and Emily. Fred doesn't actually have much of an area to live in. His little 2D plane is actually hanging on the wall of Bob's living room. Bob can walk over and observe Fred any time he likes. Fred's world has a ceiling, a front, a back, and a floor. Bob's world, actually, isn't very big either. He has a cieling, 4 walls, and a floor. His 3-D world is also hanging on a wall: in Emily's living room. Emily's world could also be hanging on someone else's wall, and so on. Here is Fred's world on Bob's wall:

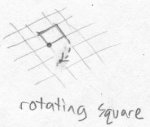
If a square is rotated in fred's world, it rotates around a single point. This means that only a single point on the square stays at its original location as the square spins around. Thus, the axis of an object in planespace is zero-dimensional.
Now imagine that Bob has Fred's world resting flat on a table. Bob has placed a cube on Fred's 2d world, as if the cube is a paperweight to hold down Fred's world from fluttering away in the wind. Fred's world is sandwiched between the table and the cube paperweight. The bottom surface of the cube, which is intersected with Fred's world, appears to Fred to be a simple square. If this cube is rotated, it appears to Fred as though a square is rotating around a point. In reality, it is a cube rotating around a line, whose axis extends perpendicular to Fred's world from the point of rotation. This means that all of the points along the axis will stay at their original location as the cube spins, but every other point in the cube will move in a circle. Thus, the axis of an object in realmspace is one-dimensional.

Now imagine that Emily lays Bob's world flat on a tetral table. The direction towards the table from Bob's world is delta (down in tetraspace), and the opposite direction into the air above the table is upsilon (up in tetraspace). Emily places a tetracube on top of Bob's world on the upsilon side of it. Bob's world is now sandwiched between the tetral table and the tetracube. The tetracube is intersected with Bob's world, so Bob sees a cube floating in mid-air. Now let's say that Emily rotates her tetracube around one of it's edges. Bob will only see a cube rotating, but the tetracube it's attached to is rotating with it. The axis of rotation for the tetracube isn't a line, though. It's a plane formed by extending the linear edge of the cube into Emily's world, perpendicular to realmspace. All of the points on this square stay in place as the tetracube rotates in tetraspace. Thus, the axis of an object in tetraspace is two-dimensional.
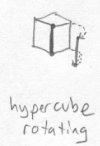
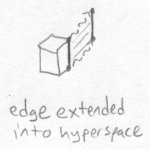
Imagining how the linear axis of a cube could extend into tetraspace is hard. We can try to picture it by imagining its axis shifting off in a random direction as pictured below, even though this isn't what is truly happening:
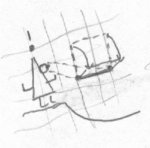
Fred is sitting in his living room the next day, and there is a square object floating in front of him in mid-air. Bob decides to play a trick on Fred. He grabs an edge of the square and pulls it into realmspace, leaving a linear edge in Fred's universe remaining. Fred only sees a line left of the original square. Here is what Bob just did:
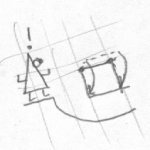
Bob completes the rotation and places the square fully back into Fred's world. But, now the edge that had disappeared is on the opposite side. Fred is now astonished to see that the square has been completely inverted. Such an action would be impossible in a two dimensional world. Fred tries to invert the square back to its normal state, but no matter how many times he turns the square around, it doesn't work:
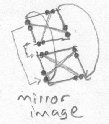
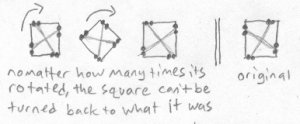
The square has become its mirror image, with its left and right sides swapped. Fred has difficulty understanding how this could have happened to his square. The first way he tries to imagine it is to imagine that one of the sides has been pushed through the middle of the square and to the opposite side, making everything inverted. This is how he imagines it:
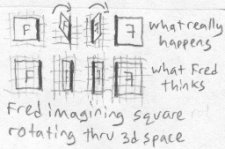
Fred contemplates what happened some more, but can't quite wrap his mind around it. He thinks about another way it might have happened. One side could have been shifted upwards and towards the other one until one side was above the other, then shifted further until it came into place on the other side. The moved side would have made a half circle around the side that stayed. Here is how he imagines it this time:
But, this is not what really happened. It is merely a futile attempt of Fred's to understand what's happened in the third dimension using only what he knows of the second dimension. The effects of Bob's actions are easy to see, but explaining them to Fred is not.
Emily sees what Bob did to Fred, and decides to play a similar trick on him. Bob is sitting on his floor staring at a box that he has just filled with his favorite sentimental possessions, when all of a sudden the whole box except one of its sides disappears. Here is what he sees:
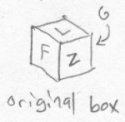
He stares at it astonished, and is even more surprised when all of a sudden the rest of the box appears again. But, the box has just appeared on the opposite side of the face that had remained. All of the lettering on the box has been turned into its mirror image. Here is what the box looks like afterwards:

Bob looks into the box, and finds that something has happened to all the letters in the books that were in the box - they are all their mirror images! He takes one of the books and puts it up to a mirror, and finds that the mirror reverses the letters back to their original state. As Fred did, Bob tries to understand how this could possibly occur. He tries to imagine one side of the box being squished into its opposite side, but being pushed further until it comes into place on the other side of the box from where it was before. All of the letters have been inversed:
This is analogous to Fred's solution with the disappearing side being squished through the remaining side. It isn't what really happened in tetraspace, though. Bob contemplates further, and again conceives of another idea like Fred did. Maybe one face of the box was shifted in a half circle around the side that remained. All the letters would end up being reversed just like in the previous theory:
As we know by looking at Fred's example, the size and shape of the square don't actually change as it's rotated through realmspace. The only ways that Fred has thought of to explain what happened involve the square changing shape. The real event doesn't require the square to change shape at all. It is the same situation with the cube. As it is rotated through tetraspace, the actual shape of it isn't changed at all; it remains a perfect cube. The only way we can imagine the result, however, is by distortions in realmspace.

Bob doesn't realize it yet, but he is also exposed. Emily can see every part of his world at once. She can see inside his tightly locked safe, into his refridgerator, into his desk drawers, and she can see his insides. Bob is basically naked to Emily, even though he feels fully clothed. She can touch any part of his insides without having to go through his skin or his clothes.
One day, Bob is feeling particularly devious and decides to remove the contents out of Fred's safe. He walks over to Fred's world, removes Fred's money from inside the safe and sticks it onto Fred's table. Bob doesn't have to open the safe because he can just bring it out of planespace into realmspace, move it, and then put it back into planespace. The money doesn't have to go through the walls of the safe because it can just pass "over" its walls in realmspace.
Fred comes in from a leisurely walk in the woods and is astonished to see all his money lying on the table. He was sure he had put it in the safe the night before. He checks out his safe, but nothing has happened to it. He opens it up, and it's empty. He sticks the money back into the safe, and makes sure it's closed securely. As soon as Fred closes the safe, Bob grabs the money again and puts it on the table behind Fred. Fred turns around to see the money he had just secured now lying behind him. Now Fred thinks he is going crazy.
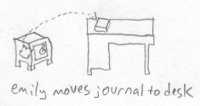
Emily has seen what Bob did to Fred, so she decides to teach him a lesson by doing the same thing to him. Bob has his journal locked up in his safe, which has both a combination lock and a key lock on it. Bob knows his safe is secure because he bought the best safe on the market and only he knows the combination to it. Emily removes the book from the safe by pulling it into tetraspace. She moves it over to Bob's desk and reinserts it back into realmspace. The book didn't have to go through the walls of the safe because it could go "over" its walls in tetraspace.
Bob is reading another book and looks up to see his journal sitting right in front of him. He is quite stunned and confused, because he was sure he had put the journal into his safe. He checks out the safe, and there seems to be nothing wrong with it. He takes the journal and puts it back into his safe, making sure it's definitely locked. He even ties a rope around the safe so that he can see if anyone tampers with it. He returns to his desk and resumes his reading. Emily grabs the journal again, moving it to tetraspace and inserting it back on the table in front of him. When Bob looks down and sees the journal in front of him again, he thinks he is going crazy. He looks back to see the rope still tied around the safe, exactly the way he left it. Then he remembers what he did to Fred, and realizes that someone else may be doing the same thing to him.
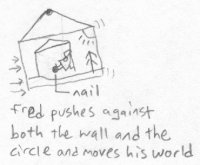
Bob decides to have some more fun and tease Fred again. Fred's world is hanging on Bob's wall, but not tightly. Bob takes a nail, and right in front of Fred's view, he hammers the nail right through Fred's world. All of a sudden Fred sees a circle appear in midair. He decides to investigate, so he grabs it and tries to move it, but it won't move. It is thoroughly fastened in mid air.


This is rather bizarre and he decides to try some things with the floating circle. He sits against a wall of his house and pushes against the circle with his feet. It requires a lot of effort, but the circle moves. It feels like he is holding up the whole world, and in reality that is what he is doing. When Fred lets go of the circle, it swings back to its original position and Fred falls to the ground.
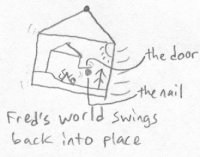
Bob removes the nail, so Fred sees the circle suddenly vanish. Bob raises Fred's safe into the air and drives a nail through the middle of it. He lets it go, and the safe hangs in mid air on the nail. The nail didn't have to go through any of the walls of the safe in order for the safe to be hanging. The nail just went through the air through the inside of the safe. This is similar to hanging a loop with a nail on the wall in realmspace - the loop itself doesn't have to be pierced, but the nail has to go through the area in the middle of the loop.
To Fred, the circle was just a strange object hanging in mid-air, but now Fred's own safe is hovering. Fred opens his safe and looks inside, and to his surprise he sees that the circle has reappeared, but now his safe is hanging on it. Fred removes the safe from the "hook" and puts it back on the ground. This has been enough bizarre events for one day, so he goes outside to get a breath of fresh air.



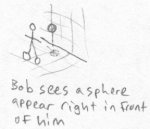
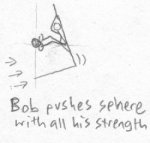
Emily sees that Bob hasn't learned his lesson. She does the same type of thing to Bob with the hope that Bob will realize what's happening to him. She has Bob's world hanging on her wall and she drives a "tetranail" (four-dimensional nail) through his world. Bob sees a sphere suddenly appear in midair near a wall. He remembers what he just did to Fred, and to test out his hypothesis he does the same thing that Fred did. He sits back against the wall and pushes against the sphere with all his strength. He succeeds in pushing it a few inches, but it requires a lot of effort. When he lets go, the sphere swings back to its original position and he falls on the floor. Bob is starting to realize that something else is out there.

Emily also performs the "Levitating Safe" trick. She raises Bob's safe into the air and drives the tetranail through the air in the middle of it. Emily didn't have to pierce any of the sides of the safe in order to hang the Bob's safe on her wall. Bob opens the safe and sees that the safe is hanging on the sphere, just like Fred's safe was hanging on the circle. He pulls the safe off of the levitating sphere and places it back on the floor.

Emily decides to play another trick on Bob. Bob has a plant hanging from his ceiling by a chain. Emily holds the plant in the air while she pulls one of the chain links into tetraspace. She puts the chain link back into realmspace at a different location and lets both the plant and the chain link drop to the floor. Bob sees this and walks over cautiously to inspect the scene. He sees a plant on the ground with dirt everywhere, a single chain link intact sitting next to the plant, and the rest of the chain hanging from the ceiling, intact. None of the chains had to be bent or broken open for Emily to perform her trick. Bob couldn't have played this particular trick on Fred because chains aren't possible in planespace.
Bob decides to continue playing tricks on Fred so that he can see what the equivalent is in his own world. Bob decides to try rocking Fred's world back and forth along the wall. Since Fred's world is swaying back and forth, he can't hold his balance and falls over. One surface of Fred's world scrapes against the wall, but on the other side is only in contact with the air in Bob's world. Fred's world can only move two directions and still be in contact with the wall. If Fred's world is moved in a third direction (outward), it is no longer in contact with Bob's wall.

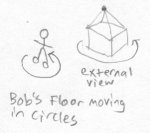
Emily watches what Bob has done and does the same thing to Bob. She has 4 directions she can push Bob's world to and still have it scrape against her wall. First she pushes it front and back, then left and right. To Bob it feels like there's an earthquake happening. Emily stops Bob's world from moving, then starts it moving around in circles. This whole time, all of Bob's world is scraping against Emily's wall, not falling off. If Emily moves Bob's world in a fifth direction (outward), then it is no longer in contact with her wall.

In order to give you a better understanding the fourth dimension, I will begin with a method that follows a sequence of n-hypercubes that starts with the zeroth dimension and progresses up to the fourth dimension. An n-hypercube is the generalization of the cube within n dimensions, with a 3-hypercube just being the traditional cube. By seeing each n-hypercube build up from the previous one, you should have a better understanding of the final step, from the third dimension to the fourth dimension.
Step 1 - Zeroth Dimension. Imagine a point in space. It is a 0-hypercube. A point is zero dimensional because it has no width, length, or height, and is infinitely small. Every point is exactly the same and has the same measurements, because it has no dimension. Below is a picture of a point, representing the zeroth dimension.

Step 2 - First Dimension. Take the zero-dimensional point and extrude it in any direction, creating a line segment, which is a 1-hypercube. All line segments are one-dimensional because they differ in size by only one measurement, length. They all have the same width and height, which is infinitely small. If you expanded the line infinitely, it would cover one-dimensional space.

Step 3 - Second Dimension. Now take the line segment and extrude it in any direction that is perpendicular to the first direction, creating a square, which is a 2-hypercube. All squares are two dimensional because they differ with each other in size by two measurements, width and length. They all have the same height, which is infinitely small. All of the edges are the same length, and all of the angles are right angles. If you expanded the square infinitely, it would cover two-dimensional space.

Step 4 - Third Dimension. Take the non-infinite square and extrude it in a third direction, perpendicular to both of the first two directions, creating a cube, which is a 3-hypercube. All cubes are three dimensional because they differ with each other in size by all of the three measurements that we know of - width, length, and height. Just like the square, all of the edges within a single cube are the same length, and all of the angles are right angles. If you expanded the cube infinitely in all directions, it would cover three-dimensional space.

Step 5 - Fourth Dimension. Now, the final step. Take the non-infinite cube and extrude it in yet another direction perpendicular to the first three. But how can we do this? It is impossible to do within the restrictions of the third dimension (which will I refer to as realmspace in this webpage). However, within the fourth dimension , it is possible. The shape that results from this extrusion of a cube into tetraspace is called a tesseract, which is a 4-hypercube. All tesseracts differ from other tesseracts in size by four measurements - width, length, height, and a fourth measurement, which I call trength. Looking back to the previous n-dimensional cubes, they all have the same trength, which is infinitely small. Just like the cube and square, all of the edges within a single tesseract are the same length, and all of the angles are right angles. If you expanded the tesseract infinitely, it would cover four-dimensional space.
There are several ways to view the tesseract, and I will show three of them here. The first one is called an inner projection, and it is formed from a projecting the tesseract into realmspace with a perspective projection. The parts of the original tesseract that are farther away appear smaller in the inner projection. The original cube cell that existed before the extrusion into a tesseract is in gray, the paths of the vertices are in teal, and the stopping point of the extruded cube cell is in blue. The real tesseract isn't shaped like the inner projection shown below - the inner projection is a very distorted "image" of the original tesseract. All of the edges you see in the image are actually the same length as each other, and all angles between edges are right angles.

The second way to view a tesseract isn't actually a normal tesseract, but a parallel projection of a skewed tesseract. To make this shape, first you make a tesseract, then shift the top cube cell a short distance in a diagonal direction, parallel to realmspace. Since this shift is parallel to realmspace, it can actually be in any direction that you can point to. After the shift, you trace the shadow of the skewed tesseract's edges. The result is a shape that has two cubes with their vertices connected together. In the orignal shape, all of the edges within the cube cells are the same length and have right angles with each other. However, they don't have right angles with the teal connection edges, and the teal connection edges are slightly longer than the cube cells' edges.

The third way to view a tesseract is a parallel projection into realmspace. It is the same as a skewed tesseract, but without the top cube cell shifted. Since the edges of the tesseract were extruded in a direction perpendicular to realmspace, when the shape is projected back into realmspace, the edges of the blue cube cell are projected straight back onto the gray cube cell's edges. The resulting projection is a simple cube. This didn't happen with the inner projection, because that projection was a perspective projection.

This last step of trying to view a tesseract shows the difficulties in portraying objects from tetraspace within the limitations of realmspace - there is an extra perpendicular direction that we can't depict within our own space without distorting the original object. Because of these problems, it takes many examples in order to begin understanding the nature of the fourth dimension.
four dimensional space) is a fascinating place. Events that would be bizarre and mind-bending to us puny little realmic beings would be common-place and taken for granted in tetraspace. Jumping straight into thinking about tetraspace is enough to boggle any human mind. An indirect route must be taken if there is any hope of understanding the possibilities of tetraspace. The method I use here is the one pioneered by the books Flatland and Sphereland, and is the one used in just about every other text about the fourth dimension. First, the I tell of the adventures of a planar being (a two-dimensional being) attempting to understand realmspace. Going from planespace (two-dimensional space) to realmspace will shed light on how to conceptualize going from realmspace to tetraspace. While going from planespace to realmspace may seem overly simple, it is necessary to understand exactly what is happening so that you can understand the process of going from realmspace to tetraspace.
Just as tetraspace is mind-boggling to us realmic beings, realmspace is mind-boggling to planar beings. Things we take for granted are extremely difficult for planar beings to conceptualize. The only thing a planar being can see of our realmic objects is their planar cross sections in his planespace, and the effects of them rotating. At first, he will only be able to conceptualize the effects in planespace of realmic objects. He will only see planar objects in his mind. Eventually, with much deep thought and introspection, he may be able to conceptualize the realmic object itself. Similarly, when starting to think about tetraspace, we will only be able to conceptualize the effects of tetral (four-dimensional) objects in realmspace. We will only be able to see realmic objects in our mind at first. But, by the effects we see, we can carve a sculpture in our minds of how the full object really looks like, and conceptualize the whole of the tetral object.
The name of our planar subject is "Fred". He lives in a plane called Flatland. The only directions that Fred knows of are forward, backward, up, and down. Fred has no concept of right or left. His viewing area is merely a vertical line. Here is a picture of Fred in his native habitat:

Since Fred's viewing area is only a line, he can't see as much at once as we can. Here is the view that Fred would see if he was in the picture above:

Unfortunately for Fred, he can't see backwards - he can only see forwards. It is impossible for him to simply spin around and face the opposite direction. It is easy for beings in realmspace to face a different direction because they can just spin around, left or right. The only way for beings in planespace to face a different direction though is to turn their head down and heels up. Fred either has to stand upside down to be able to see what is behind him, or he has to walk backwards blind because he only has an eye on his front side.

Fred's writing system is very rudimentary, since a linear surface doesn't allow much detail. His writing system looks somewhat like Morse code. Here is what a page from one of his books looks like, in his view:


Fred understands the concept of a square. It can be imagined as a series of lines stacked side by side, so that the resulting shape has four sides. He has no concept of what a cube would look like, though. The best he could do is imagine a succession of squares next to each other. As you can see, this is far from the actual representation of a cube. A cube is a series of squares stacked on on top of the other:



Fred also understands what a circle looks like. It can be imagined as a series of lines stacked side by side in the way that a square is formed, but the lines start small and expand to a certain size, then shrink down again at other side.

Fred can't understand what a sphere really looks like, though. He can imagine it as a series of circles, starting small and expanding, then shrinking down again. Here is how he might picture it:

Or, he might decide to picture it as a group of concentric circles (circles with the same center):


But, as you can see, that's not really what a sphere looks like. Now imagine Fred one day is sitting in his living room, and a sphere from realmspace passes through the air right before his eyes. To him, it will appear as if a circle appeared out of nowhere in front of him. It expands rapidly, and Fred fears that it is going to devour him and his house with him. But to his relief, its growth slows down and stops. Then, the circle starts shrinking again, but slowly. Then it starts to shrink faster and faster until it quickly disappears. Here is what the event looks like:
From the third dimension to the fourth dimension

In realmspace, there is a character named Bob. He is basically your average guy - two legs, two eyes, a brain, all the usual body parts. His view of his world is a 2 dimensional plane, one dimension more than Fred has. Here is Bob in his native habitat, and his view of that habitat:


Since Bob has one dimension more than Fred has, his writing system can be more elaborate. He can write on a 2 dimensional surface. Instead of only one line of text on a page, there can be multiple lines. This allows a lot more text to me stored in a realmic book. Here is what a page from one of his books looks like:

Bob fully understands the concept of a cube. A cube is a sequence of squares laying top to bottom flat on top of each other. For any one square in this cube, every point on one surface of the square touches every other point on the surface of the square above it, and on the other side, touches every point on surface of the square below it. Here is an illustration:

Bob also understands the concept of a sphere. A sphere is a sequence of concentric circles laying top to bottom on each other, as with a square. Like a square, adjacent slices of the circle touch each other at every point. Here is an illustration:

Bob has troubles imagining a tetracube, however. Here is the best he can do to imagine a tetracube:

A tetracube is actually a sequence of cubes, where every part of a cube in this tetracube (all the insides of it) touch all the insides of the cube to its right and to its left (or its up and down, or its front and back). In actuality, the direction of the adjacent cubes are not imaginable in terms of 3d directions. I will call one of the directions into tetraspace Upsilon (for up) and the other Delta (for down).
If Bob was viewing Fred's planar world, he would see that there are two sides to it. Bob could either be on top of Flatland or below it, but in order to get to the other side, Bob must go through Flatland. There is no other way to get to the other side. Planespace separates realmspace into two separate parts. In the same way, a tetral character (Let's call her Emily) would see that she is on one side of realmspace, and she'd have to pass through Bob's world to get to the other side of it. Realmspace separates tetraspace into two separate parts.
In the first illustration below, an arrow shows the path from one side of Flatland to the other. If the arrow was an object, Fred would only see a small point. In the second illustration, a tetral arrow that passes from one side of realmspace to the other would intersect realmspace with a small point. Bob doesn't see any other part of the arrow but this:


One day, Bob is innocently sitting in his living room (as Fred was that one day), and all of a sudden, in the middle of the air, a sphere appears and grows rather rapidly. Its size levels off at a point, then starts shrinking slowly. Its shrinking quickens until it completely disappears. Bob just experienced the passage of a tetrasphere (four dimensional sphere) through realmspace.
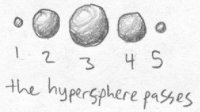
Rotation
Below is a table showing the relation between the dimensions:| person | dimension | view | axis of rotation |
| --- | 1st | point(0D) | *no rotation* |
| Fred | 2nd | line(1D) | point(0D) |
| Bob | 3rd | plane(2D) | line(1D) |
| Emily | 4th | realm(3D) | plane(2D) |

If a square is rotated in fred's world, it rotates around a single point. This means that only a single point on the square stays at its original location as the square spins around. Thus, the axis of an object in planespace is zero-dimensional.

Now imagine that Bob has Fred's world resting flat on a table. Bob has placed a cube on Fred's 2d world, as if the cube is a paperweight to hold down Fred's world from fluttering away in the wind. Fred's world is sandwiched between the table and the cube paperweight. The bottom surface of the cube, which is intersected with Fred's world, appears to Fred to be a simple square. If this cube is rotated, it appears to Fred as though a square is rotating around a point. In reality, it is a cube rotating around a line, whose axis extends perpendicular to Fred's world from the point of rotation. This means that all of the points along the axis will stay at their original location as the cube spins, but every other point in the cube will move in a circle. Thus, the axis of an object in realmspace is one-dimensional.

Now imagine that Emily lays Bob's world flat on a tetral table. The direction towards the table from Bob's world is delta (down in tetraspace), and the opposite direction into the air above the table is upsilon (up in tetraspace). Emily places a tetracube on top of Bob's world on the upsilon side of it. Bob's world is now sandwiched between the tetral table and the tetracube. The tetracube is intersected with Bob's world, so Bob sees a cube floating in mid-air. Now let's say that Emily rotates her tetracube around one of it's edges. Bob will only see a cube rotating, but the tetracube it's attached to is rotating with it. The axis of rotation for the tetracube isn't a line, though. It's a plane formed by extending the linear edge of the cube into Emily's world, perpendicular to realmspace. All of the points on this square stay in place as the tetracube rotates in tetraspace. Thus, the axis of an object in tetraspace is two-dimensional.

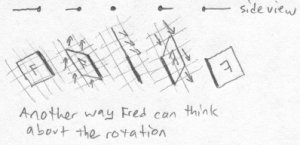
Imagining how the linear axis of a cube could extend into tetraspace is hard. We can try to picture it by imagining its axis shifting off in a random direction as pictured below, even though this isn't what is truly happening:

Fred is sitting in his living room the next day, and there is a square object floating in front of him in mid-air. Bob decides to play a trick on Fred. He grabs an edge of the square and pulls it into realmspace, leaving a linear edge in Fred's universe remaining. Fred only sees a line left of the original square. Here is what Bob just did:

Bob completes the rotation and places the square fully back into Fred's world. But, now the edge that had disappeared is on the opposite side. Fred is now astonished to see that the square has been completely inverted. Such an action would be impossible in a two dimensional world. Fred tries to invert the square back to its normal state, but no matter how many times he turns the square around, it doesn't work:



The square has become its mirror image, with its left and right sides swapped. Fred has difficulty understanding how this could have happened to his square. The first way he tries to imagine it is to imagine that one of the sides has been pushed through the middle of the square and to the opposite side, making everything inverted. This is how he imagines it:

Fred contemplates what happened some more, but can't quite wrap his mind around it. He thinks about another way it might have happened. One side could have been shifted upwards and towards the other one until one side was above the other, then shifted further until it came into place on the other side. The moved side would have made a half circle around the side that stayed. Here is how he imagines it this time:

But, this is not what really happened. It is merely a futile attempt of Fred's to understand what's happened in the third dimension using only what he knows of the second dimension. The effects of Bob's actions are easy to see, but explaining them to Fred is not.
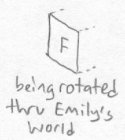
Emily sees what Bob did to Fred, and decides to play a similar trick on him. Bob is sitting on his floor staring at a box that he has just filled with his favorite sentimental possessions, when all of a sudden the whole box except one of its sides disappears. Here is what he sees:


He stares at it astonished, and is even more surprised when all of a sudden the rest of the box appears again. But, the box has just appeared on the opposite side of the face that had remained. All of the lettering on the box has been turned into its mirror image. Here is what the box looks like afterwards:

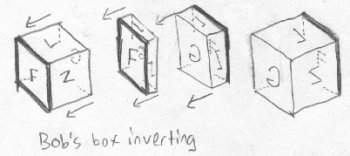
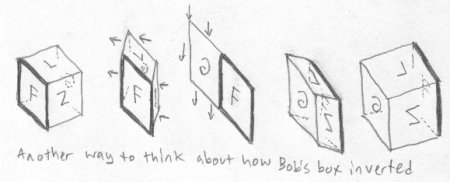
Bob looks into the box, and finds that something has happened to all the letters in the books that were in the box - they are all their mirror images! He takes one of the books and puts it up to a mirror, and finds that the mirror reverses the letters back to their original state. As Fred did, Bob tries to understand how this could possibly occur. He tries to imagine one side of the box being squished into its opposite side, but being pushed further until it comes into place on the other side of the box from where it was before. All of the letters have been inversed:

This is analogous to Fred's solution with the disappearing side being squished through the remaining side. It isn't what really happened in tetraspace, though. Bob contemplates further, and again conceives of another idea like Fred did. Maybe one face of the box was shifted in a half circle around the side that remained. All the letters would end up being reversed just like in the previous theory:

As we know by looking at Fred's example, the size and shape of the square don't actually change as it's rotated through realmspace. The only ways that Fred has thought of to explain what happened involve the square changing shape. The real event doesn't require the square to change shape at all. It is the same situation with the cube. As it is rotated through tetraspace, the actual shape of it isn't changed at all; it remains a perfect cube. The only way we can imagine the result, however, is by distortions in realmspace.
Flatness and Levitation
When Bob watches Fred's world, he can see every point in his world at once. He can see Fred's insides, what's inside his safe, what's underground, where the quarter he lost is, everything. Fred is basically naked to Bob, even though he has clothes on. Bob would be able to touch Fred's insides without having to go through Fred's skin, and there's nothing Fred would be able to do about it to stop him.
Bob doesn't realize it yet, but he is also exposed. Emily can see every part of his world at once. She can see inside his tightly locked safe, into his refridgerator, into his desk drawers, and she can see his insides. Bob is basically naked to Emily, even though he feels fully clothed. She can touch any part of his insides without having to go through his skin or his clothes.
One day, Bob is feeling particularly devious and decides to remove the contents out of Fred's safe. He walks over to Fred's world, removes Fred's money from inside the safe and sticks it onto Fred's table. Bob doesn't have to open the safe because he can just bring it out of planespace into realmspace, move it, and then put it back into planespace. The money doesn't have to go through the walls of the safe because it can just pass "over" its walls in realmspace.
Fred comes in from a leisurely walk in the woods and is astonished to see all his money lying on the table. He was sure he had put it in the safe the night before. He checks out his safe, but nothing has happened to it. He opens it up, and it's empty. He sticks the money back into the safe, and makes sure it's closed securely. As soon as Fred closes the safe, Bob grabs the money again and puts it on the table behind Fred. Fred turns around to see the money he had just secured now lying behind him. Now Fred thinks he is going crazy.

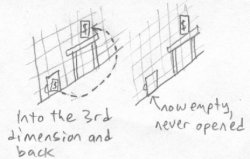
Emily has seen what Bob did to Fred, so she decides to teach him a lesson by doing the same thing to him. Bob has his journal locked up in his safe, which has both a combination lock and a key lock on it. Bob knows his safe is secure because he bought the best safe on the market and only he knows the combination to it. Emily removes the book from the safe by pulling it into tetraspace. She moves it over to Bob's desk and reinserts it back into realmspace. The book didn't have to go through the walls of the safe because it could go "over" its walls in tetraspace.
Bob is reading another book and looks up to see his journal sitting right in front of him. He is quite stunned and confused, because he was sure he had put the journal into his safe. He checks out the safe, and there seems to be nothing wrong with it. He takes the journal and puts it back into his safe, making sure it's definitely locked. He even ties a rope around the safe so that he can see if anyone tampers with it. He returns to his desk and resumes his reading. Emily grabs the journal again, moving it to tetraspace and inserting it back on the table in front of him. When Bob looks down and sees the journal in front of him again, he thinks he is going crazy. He looks back to see the rope still tied around the safe, exactly the way he left it. Then he remembers what he did to Fred, and realizes that someone else may be doing the same thing to him.

Bob decides to have some more fun and tease Fred again. Fred's world is hanging on Bob's wall, but not tightly. Bob takes a nail, and right in front of Fred's view, he hammers the nail right through Fred's world. All of a sudden Fred sees a circle appear in midair. He decides to investigate, so he grabs it and tries to move it, but it won't move. It is thoroughly fastened in mid air.


This is rather bizarre and he decides to try some things with the floating circle. He sits against a wall of his house and pushes against the circle with his feet. It requires a lot of effort, but the circle moves. It feels like he is holding up the whole world, and in reality that is what he is doing. When Fred lets go of the circle, it swings back to its original position and Fred falls to the ground.


Bob removes the nail, so Fred sees the circle suddenly vanish. Bob raises Fred's safe into the air and drives a nail through the middle of it. He lets it go, and the safe hangs in mid air on the nail. The nail didn't have to go through any of the walls of the safe in order for the safe to be hanging. The nail just went through the air through the inside of the safe. This is similar to hanging a loop with a nail on the wall in realmspace - the loop itself doesn't have to be pierced, but the nail has to go through the area in the middle of the loop.
To Fred, the circle was just a strange object hanging in mid-air, but now Fred's own safe is hovering. Fred opens his safe and looks inside, and to his surprise he sees that the circle has reappeared, but now his safe is hanging on it. Fred removes the safe from the "hook" and puts it back on the ground. This has been enough bizarre events for one day, so he goes outside to get a breath of fresh air.



Emily sees that Bob hasn't learned his lesson. She does the same type of thing to Bob with the hope that Bob will realize what's happening to him. She has Bob's world hanging on her wall and she drives a "tetranail" (four-dimensional nail) through his world. Bob sees a sphere suddenly appear in midair near a wall. He remembers what he just did to Fred, and to test out his hypothesis he does the same thing that Fred did. He sits back against the wall and pushes against the sphere with all his strength. He succeeds in pushing it a few inches, but it requires a lot of effort. When he lets go, the sphere swings back to its original position and he falls on the floor. Bob is starting to realize that something else is out there.



Emily also performs the "Levitating Safe" trick. She raises Bob's safe into the air and drives the tetranail through the air in the middle of it. Emily didn't have to pierce any of the sides of the safe in order to hang the Bob's safe on her wall. Bob opens the safe and sees that the safe is hanging on the sphere, just like Fred's safe was hanging on the circle. He pulls the safe off of the levitating sphere and places it back on the floor.

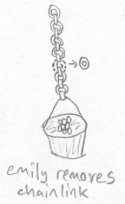
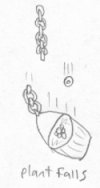
Emily decides to play another trick on Bob. Bob has a plant hanging from his ceiling by a chain. Emily holds the plant in the air while she pulls one of the chain links into tetraspace. She puts the chain link back into realmspace at a different location and lets both the plant and the chain link drop to the floor. Bob sees this and walks over cautiously to inspect the scene. He sees a plant on the ground with dirt everywhere, a single chain link intact sitting next to the plant, and the rest of the chain hanging from the ceiling, intact. None of the chains had to be bent or broken open for Emily to perform her trick. Bob couldn't have played this particular trick on Fred because chains aren't possible in planespace.


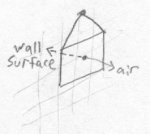
Bob decides to continue playing tricks on Fred so that he can see what the equivalent is in his own world. Bob decides to try rocking Fred's world back and forth along the wall. Since Fred's world is swaying back and forth, he can't hold his balance and falls over. One surface of Fred's world scrapes against the wall, but on the other side is only in contact with the air in Bob's world. Fred's world can only move two directions and still be in contact with the wall. If Fred's world is moved in a third direction (outward), it is no longer in contact with Bob's wall.


Emily watches what Bob has done and does the same thing to Bob. She has 4 directions she can push Bob's world to and still have it scrape against her wall. First she pushes it front and back, then left and right. To Bob it feels like there's an earthquake happening. Emily stops Bob's world from moving, then starts it moving around in circles. This whole time, all of Bob's world is scraping against Emily's wall, not falling off. If Emily moves Bob's world in a fifth direction (outward), then it is no longer in contact with her wall.


Comments